[C++][图形学]TinyRenderer第二课——2D三角形光栅化

TinyRenderer项目地址：三角形光栅化

扫描线算法，先对三角形的三个顶点按y轴进行冒泡升序排序（顶点y轴从高到低顺序为cy -> by -> ay），将三角形分为上半部分(ca和cb)和下半部分(ca和ba)，遍历y（ay -> by,by->cy）轴，获取相同y轴下左右两个线段端点的x，填充这区间(x1->x2,y)的像素点。

void triangle(int ax, int ay, int bx, int by, int cx, int cy, TGAImage &framebuffer, TGAColor color)
{
    // 对三个顶点进行冒泡排序，最终顺序cy -> by -> ay
    if (ay > by)
    {
        std::swap(ax, bx);
        std::swap(ay, by);
    }
    if (ay > cy)
    {
        std::swap(ax, cx);
        std::swap(ay, cy);
    }
    if (by > cy)
    {
        std::swap(bx, cx);
        std::swap(by, cy);
    }
    // 获取下半部分左右线段ca和ba的端点
    int total_height = cy - ay;
    int segment_height = by - ay;
    if(ay != by)
    for (int y = ay; y <= by; y++)
    {
        // 获取x点
        int xCA = ax + (y - ay) * (cx - ax) / total_height;
        int xBA = ax + (y - ay) * (bx - ax) / segment_height;
        for (int x = std::min(xCA, xBA); x < std::max(xCA, xBA); x++) // draw a horizontal line
            framebuffer.set(x, y, color);
    }
    // 获取上半部分左右线段ca和cb的端点
    segment_height = cy - by;
    if(cy != by)
    for (int y = by; y <= cy; y++)
    {
        // 获取x点
        int xCA = ax + (y - ay) * (cx - ax) / total_height;
        int xCB = bx + (y - by) * (cx - bx) / segment_height;
        for (int x = std::min(xCA, xCB); x < std::max(xCA, xCB); x++) // draw a horizontal line
            framebuffer.set(x, y, color);
    }
}

上述的扫描线算法是一种为单线程 CPU 编程设计的老派方法。

新时代的三角形光栅化算法支持多线程并行计算来提高效率。

首先用一个包围盒包裹三角形，剔除无关区域。对包围盒中的每个像素，只需要判断该像素是否在三角形呢就可。

void triangle(int ax, int ay, int bx, int by, int cx, int cy, TGAImage &framebuffer, TGAColor color)
{
    int minx = std::min(ax,std::min(bx,cx));
    int miny = std::min(ay,std::min(by,cy));
    int maxx = std::max(ax,std::max(bx,cx));
    int maxy = std::max(ay,std::max(by,cy));
    //用包围盒包围三角形，剔除大部分无用区域
    //并行计算
    #pragma omp parallel for
    for(int x = minx;x <= maxx;x++){
        for(int y = miny;y <= maxy;y++){
                framebuffer.set(x, y, color);
        }
    } 
}

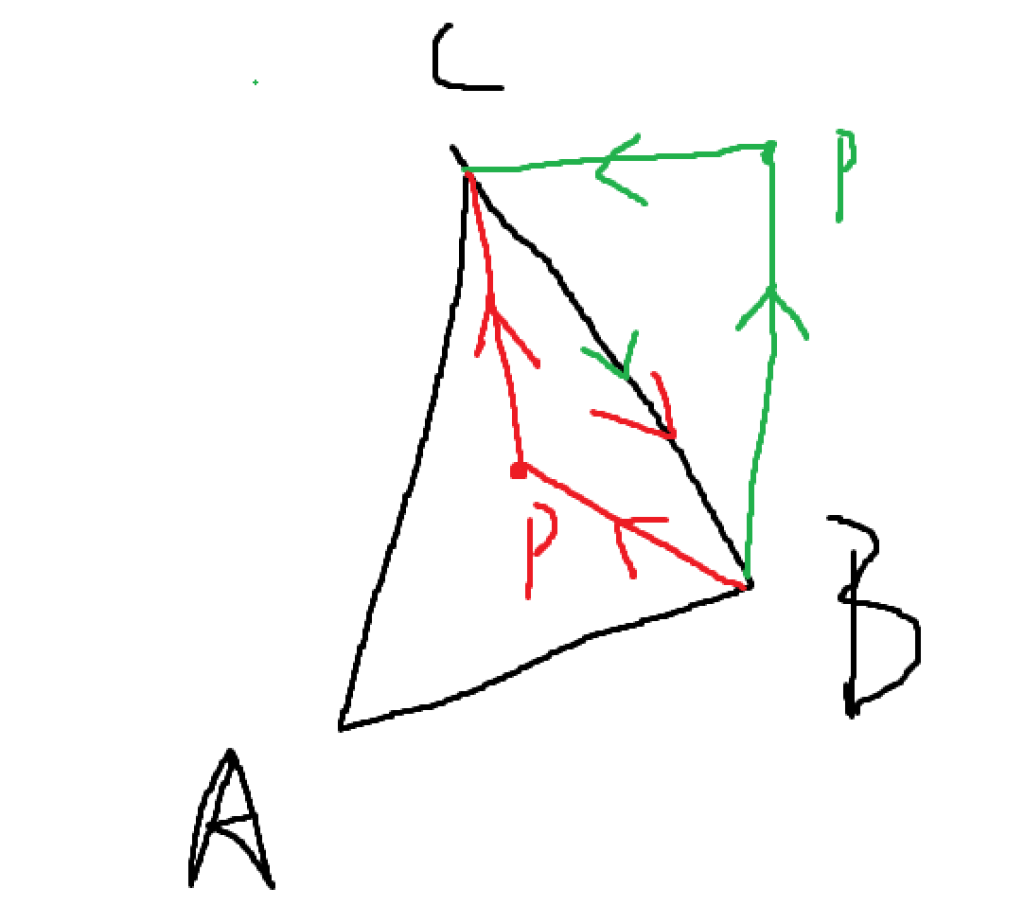
判断一个点是否在三角形内部：用重心坐标来表示一个点 P = uA + vB +wC (u+v+w =1)可以看作点P是由A,B,C三个顶点乘以不同权重得到的。对于在三角形内部的点遵循 u >= 0 && v >= 0 && w >= 0，A,B,C三个顶点都对点P有一定的贡献。因此当任意权重<0时，该点就在三角形外。用P和三个顶点构成的子三角形的面积除去总面积可得到u,v,w权重。

//计算三角形面积
double signed_triangle_area(int ax, int ay, int bx, int by, int cx, int cy) {
    return .5*((by-ay)*(bx+ax) + (cy-by)*(cx+bx) + (ay-cy)*(ax+cx));
}

void triangle(int ax, int ay, int bx, int by, int cx, int cy, TGAImage &framebuffer, TGAColor color)
{
    int minx = std::min(ax,std::min(bx,cx));
    int miny = std::min(ay,std::min(by,cy));
    int maxx = std::max(ax,std::max(bx,cx));
    int maxy = std::max(ay,std::max(by,cy));
    //用包围盒包围三角形，剔除大部分无用区域
    double total_area = signed_triangle_area(ax,ay,bx,by,cx,cy); 
    //并行计算  
    #pragma omp parallel for
    for(int x = minx;x <= maxx;x++){
        for(int y = miny;y <= maxy;y++){
            double pca_area = signed_triangle_area(x,y,cx,cy,ax,ay) / total_area;
            double pab_area = signed_triangle_area(x,y,ax,ay,bx,by) / total_area;
            double pbc_area = signed_triangle_area(x,y,bx,by,cx,cy) / total_area;
            if(pca_area < 0 || pab_area < 0 || pbc_area < 0)continue;
                framebuffer.set(x, y, color);
        }
    } 
}

其中计算三角形面积公式是有向的。如三角形PCB，若P在直线CB的左侧，则P,C,B是顺时针的顺序，求出的面积是一个整数，而当P在直线CB的右侧时，则P,C,B是逆时针的顺序，此时面积会是一个负数。由此可知当P在三角形内部时，需要满足PCB，PAB，PAC的面积都为正。上述代码中除以了总面积，总面积是由ABC的逆时针顺序计算的，所以总面积为负数，所有的子三角形也要以逆时针的顺序计算。若子三角形面积与总面积的比值为负数，则P在三角形外。

//计算三角形面积
double signed_triangle_area(int ax, int ay, int bx, int by, int cx, int cy) {
    return .5*((by-ay)*(bx+ax) + (cy-by)*(cx+bx) + (ay-cy)*(ax+cx));
}